Terremotos del 19 S: ¿Fecha maldita o casualidad no tan increíble?

¿Cuáles son las probabilidades de que tres sismos “mayores” observados en años diferentes coincidan en la misma fecha en el mismo país? La respuesta los sorprenderá.

19S: fecha maldita para unos, casualidad para otros
19S: fecha maldita para unos, casualidad para otros. La ciencia tiene la palabra.

En una reunión de amigos, muchos se asombran al descubrir que comparten el mismo signo del zodíaco. Tampoco es raro encontrar que, entre compañeros de curso en la escuela o universidad, haya coincidencia en el día y mes del cumpleaños.

En México, tres sismos de gran magnitud han coincidido en el mismo día y mes: un 19 de septiembre. El primero se registró en 1985, otro en 2017 y el último en 2022. Las redes sociales se inundaron de memes sobre la “maldición” del 19S, pero en realidad, para la ciencia esta casualidad no es tan extraordinaria.

México, tierra de sismos

Es menester señalar que los sismos no se pueden predecir, ni existe una “temporada de sismos”, o un mes donde la sismicidad es mayor. Y que no hay “Ley de Atracción” que los origine, como muchos han sugerido en esta ocasión.

La República Mexicana se encuentra en una de las regiones sísmicamente más activas del mundo. De hecho, ocurren diariamente en promedio unos 4 sismos de magnitud 3.0 o mayor. En la base de datos de 1900 a 2022 del Servicio Sismológico Nacional de México (SSN), hay registros de 260.634 sismos reportados de todas las magnitudes, todas las profundidades y en todo el país.

Mapa sismicidad México 2021
Mapa del Servicio Sismológico de México indicando los 28.340 epicentros de los sismos de magnitud 3.0 o mayores registrados en 2021

Se han registrado 18 sismos mayores a magnitud 7.0 entre 1990 y 2020. Entonces podemos decir que las estadísticas nos señalan que cada 1.66 años ocurre un sismo mayor a magnitud 7 en México. Y de acuerdo con el cálculo realizado por un especialista, la probabilidad de que tres sismos de más de 7 grados se registren en un país en tres fechas 19 de septiembre es una en 133,225, es decir, 0.000751%... algo prácticamente improbable!

Pero aquí está la trampa: nuestra intuición nos hace que pensamos que la periodicidad es una manera apropiada de calcular la probabilidad, cuando en realidad debemos tomar todos los terremotos mayores ocurridos y calcular la probabilidad de que tres de ellos hayan coincidido en el mismo día tras probar todas las combinaciones posibles.

El Problema del Cumpleaños

Si te pregunto ¿Cuánta gente crees que hace falta reunir en un evento para que al menos dos personas coincidan en la misma fecha (día y mes) de cumpleaños, cuántos dirías?

Muchas personas piensan intuitivamente un número elevado, en más de 730 personas ya que es el doble de todos los cumpleaños posibles, y eso es entendible: generalmente hay 365 días en un año. Otros pensarán intuitivamente en 183, ya que es la mitad de todos los cumpleaños posibles, por la misma razón.

Con sólo 23 personas, la chance de encontrar dos que cumplen años el mismo día es del 50%. Con 50 personas la chance es del 97%. Y con 57 personas, la chance es mayor al 99%. En este link encontrarán todo para calcular El Problema del Cumpleaños

Desafortunadamente, la intuición no es el mejor camino para resolver este tipo de problemas… y por ello muchas veces no somos tan buenos para el cálculo de probabilidades como podríamos creer.

El Problema del Cumpleaños sostiene que sólo hace falta un grupo de 23 personas para que haya más de 50% de probabilidades de que dos de ellas cumplan años el mismo día y mes.

cumpleaños, problema, probabilidad
Con sólo 23 personas, la chance de encontrar dos que cumplen años el mismo día es del 50%. Con 50 personas la chance es del 97%. Y con 57 personas, la chance es mayor al 99%.

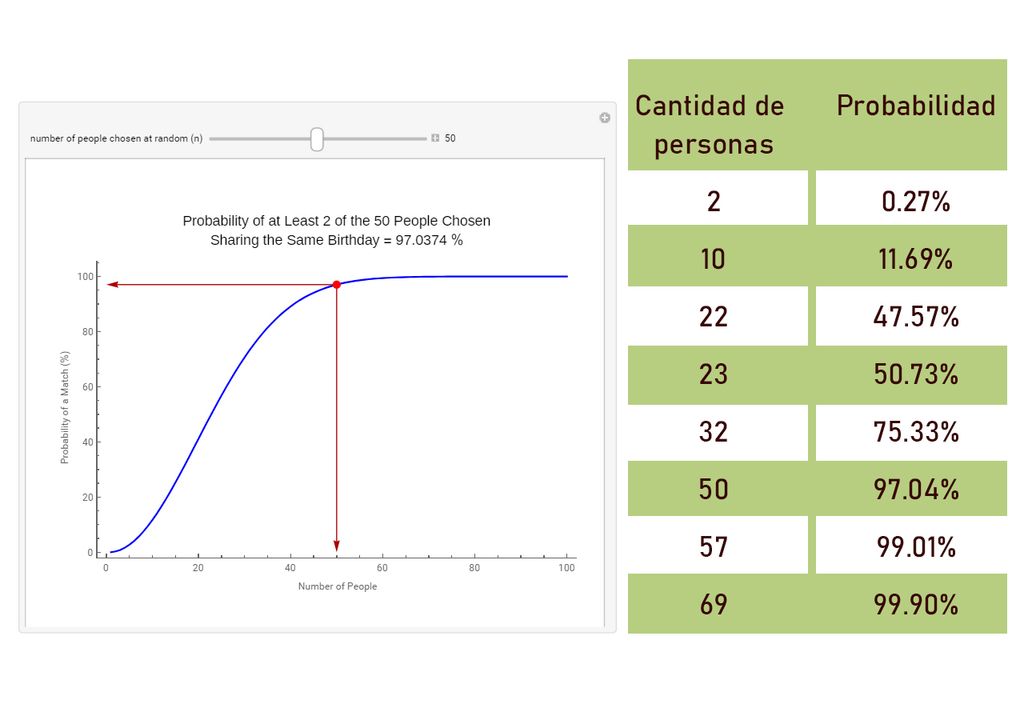
Ahora bien, si una persona se incorpora a un grupo de otras 22 personas y nos preguntáramos la probabilidad de que ella, y solo ella, cumpliera años el mismo día que cualquiera de las otras 22 personas, en ese caso la probabilidad sería muy baja, cercana a lo que dicta nuestra intuición.

El Problema del Cumpleaños en realidad estima cuál es la probabilidad de que “cualquiera” de las 23 personas puedan coincidir en su cumpleaños en “cualquier día del año”.

Para verificarlo, tomemos como ejemplo los presidentes de Argentina. Hasta ahora suman 50, por lo que la probabilidad de encontrar al menos 2 presidentes que cumplan años el mismo día y mes es del 97.04%. Y en este grupo de 50 personas encontramos cuatro pares de coincidencias:

  • 2 de abril: Luis Saénz Peña (1822) y Alberto Fernández (1959)
  • 15 de septiembre: Eugenio Lonardi (1896) y Fernando de la Rúa (1937)
  • 18 de octubre: Justo José de Urquiza (1801) y Manuel Quintana (1835)
  • 20 de noviembre: José Figueroa Alcorta (1860) y Ramón Castillo (1873)

Ahora extrapolemos este razonamiento a los terremotos mayores registrados en suelo mexicano. (NdlR: Donde dice "sismos de magnitud mayor a 7.0", podríamos reemplazarlos por "personas", para aplicar el Problema del Cumpleaños).

Si consideramos que se reportaron 86 sismos de magnitud mayor a 7.0, entonces la probabilidad de encontrar DOS sismos que coincidan en el mismo día y mes es del 99.9982%. Y la probabilidad de encontrar TRES sismos de magnitud mayor a 7.0 que coincidan en el mismo día y mes es del 51.22%

Entonces se puede afirmar que si aplicamos el Problema del Cumpleaños a los terremotos, es sencillo darse cuenta que la “extraña coincidencia” o “maldición” del 19 de septiembre no tiene nada de excepcional o maldito, sino que es cuestión de estadísticas, probabilidades y azar.